441. Arranging Coins

題目連結: 441. Arranging Coins

題目描述

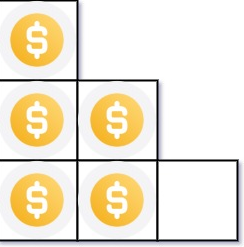
給定一個數字 n，代表有 n 個硬幣。這些硬幣將被排列成一個階梯形狀，第一行有 1 個硬幣，第二行有 2 個硬幣，依此類推。最後一行可能不完整。請計算可以完整排列的行數。

限制條件

• 1 <= n <= 2^31 - 1

思路

• 暴力解法：從 1 開始累加行數，直到總和超過 n。但時間複雜度為 O(N)，不夠高效。
• 數學解法：問題可轉化為求最大整數 k，使得 k(k + 1)/2 <= n。
• 二分搜尋：
  • 由於 n 的範圍在 1 到 2^31 - 1，我們可以在這個範圍內使用二分搜尋來尋找最大的 k。
  • 計算行數的總和公式為 k(k + 1)/2。
  • 設定搜尋範圍為 1 到 65536，因為當 k = 65536 時，k(k + 1)/2 已經超過 2^31 - 1。

解法

#define UPPER_BOUND 65536
#define SUM(x) (((long)x + 1) * x / 2)

class Solution {
public:
    int arrangeCoins(int n) {
        // i * (i - 1) / 2 < n <= (1 + i) * i / 2
        int i = 1;
        int j = UPPER_BOUND;
        while (i <= j) {
            int mid = i + (j - i) / 2;
            long sum = SUM(mid);
            if (sum == n) {
                return mid;
            }

            if (sum > n) {
                j = mid - 1;
            } else {
                i = mid + 1;
            }
        }

        return j;
    }
};

時間與空間複雜度分析

• 時間複雜度：O(1)
  • 雖然二分搜尋的時間複雜度通常為 O(log N)，但在這題中，n 的最大值為 2^31 - 1，因此二分搜尋的最大迭代次數為 log_2(65536) = 16，可以視為常數級別的時間複雜度。
• 空間複雜度：O(1)
  • 僅使用了固定數量的變數，沒有使用額外的資料結構，空間複雜度為常數。